Enseñar con Problemas

Enseñar con problemas

Sobre los problemas

Un problema es una situación en la cual se pretende llegar a una meta y, en función de lograrlo, se deben hallar y utilizar medios y estrategias. La mayoría de los problemas tienen una serie de elementos compartidos: un estado inicial, una meta a lograr, un conjunto de recursos, unas indicaciones en torno a lo que está permitido hacer y utilizar y lo que no, un dominio sobre el que se aplica y, por último experiencias de casos similares. En términos generales:

“un problema surge cuando existen obstáculos entre una situación dada y la situación a la que se quiere llegar, es querer encontrar un camino para poder llegar del estado actual al estado final, o al que se quiere obtener” (Torres, 2011:64).

Los problemas son situaciones que ubican a quien los resuelve ante la necesidad de desplegar su actividad cognitiva en un intento de búsqueda de estrategias, de elaboración de conjeturas y de toma de decisiones (Azcue, Diez, Lucaneray Scandroli, 2006). Cuando se resuelven problemas desde una disciplina, se utilizan estrategias específicas de esta (por ejemplo, en problemas matemáticos se usan estrategias propias del área). Pero también se dispone de estrategias generales: una de ellas es la heurística, que se basa en el uso de reglas empíricas para llegar a una solución.
George Pólya fue un matemático destacado que en gran parte de su vida académica se dedicó a investigar en el área de resolución de problemas. Es considerado pionero en la temática por sus aportes, que se basan en una perspectiva global y para nada restringida a las matemáticas. Pólya enfocó la resolución de problemas desde un punto de vista que permitió plantear una serie de procedimientos que se aplican en la vida cotidiana:

“Mi punto de vista es que la parte más importante de la forma de pensar que se desarrolla en matemática es la correcta actitud de la manera de acometer y tratar los problemas. Tenemos problemas en la vida diaria, en las ciencias, en la política, tenemos problemas por doquier. La actitud correcta en la forma de pensar puede ser ligeramente diferente de un dominio a otro, pero solo tenemos una cabeza y por lo tanto es natural que en definitiva haya solo un método de acometer toda clase de problemas. Mi opinión personal es que lo central en la enseñanza de la matemática es desarrollar tácticas en la resolución de problemas.”. (Pólya, 1969)

Para Pólya (1945), la heurística es el área que trata de comprender el método que conduce a la solución de problemas y, en particular, se centra en las operaciones mentales útiles en este proceso. La heurística hace uso de la sistematización de la experiencia de resolver problemas a partir de cómo lo hacen los expertos.

Para ello se propone una serie de cuatro pasos:
1. Comprender el problema. Reconocer qué se pregunta, identificar lo que hay que resolver y las condiciones asociadas
2. Elaborar un plan. Se trata de establecer la vinculación entre los datos presentes y el problema a resolver, determinar los recursos que se utilizarán, verificar la similitud con otros problemas previamente resueltos y también la posibilidad de utilizar teorías o modelos útiles, todo esto en función de buscar una manera de resolver el problema.
3. Ejecutar el plan. Desarrollar el resultado de la respuesta, a partir de ejecutar el plan, avanzando y verificando cada paso.
4. Revisar y verificar la solución. Controlar qué hace y que dice el resultado, con vistas a considerar la posibilidad de transferir la solución a otros problemas.

Etapas del método Pólya de resolución de problemas

Cada una de las etapas anteriores se ejecuta en forma de secuencia. A cada etapa, para su mejor comprensión, se le asocian una serie de preguntas orientadoras:

1. Comprender el Problema.

Etapa en la que se identifica qué se pide de modo completamente independiente de las diversas condiciones impuestas y limitaciones asociadas al problema. En particular, se determina cuál es el objetivo de trabajo, los datos con que cuentan las condiciones, y la incógnita u objetivo de trabajo.
¿Es claro el enunciado?
¿Podés replantear el problema con tus palabras?
¿Cuál es la incógnita o el objetivo de trabajo?
¿Cuáles son los datos?
¿Cuál es la condición?
¿Hay suficiente información? ¿Está presentada de manera comprensible? ¿Es la condición suficiente para determinar la incógnita?, ¿es insuficiente?, ¿es redundante?, ¿es contradictoria?
¿Es un problema similar a algún otro que haya resuelto con anterioridad?

2. Elaborar un Plan.

Se centra en el cómo o, en otras palabras, qué estrategia se va a utilizar a fin de resolver el problema. Las estrategias pueden plantearse a partir de pruebas de ensayo y error o hasta desarrollar una táctica que permita llegar a la solución. Por ejemplo, idear un plan en matemáticas, en general, se traduce en usar una ley, una definición o un principio que permita obtener la respuesta del problema. La etapa de planificación debe relacionarse con problemas parecidos, del mismo tipo, y también con resultados útiles. Se debe determinar si se pueden usar problemas similares o sus resultados (problemas análogos).

¿Te has encontrado con un problema semejante?
¿Has visto el mismo problema planteado en forma ligeramente diferente?
¿Conocés algún problema relacionado?
¿Conocés algún teorema que te pueda ser útil?
¿Podrías enunciar el problema en otra forma?
¿Podrías plantearlo en forma diferente nuevamente?

3. Aplicar el plan.

Es la puesta en práctica de lo que el estudiante estableció en la etapa anterior. Se llevan adelante las etapas planteadas. Puede suceder que en el desarrollo se detecte que algo no es pertinente para la solución del problema, lo que implicará replantear la estrategia y volver a comenzar.
¿Se pueden ver claramente que los pasos son correctos?
¿Es posible demostrarlo?

4. Revisar y verificar la Solución.

Al final del trabajo, es necesario verificar el resultado obtenido y el proceso de solución desarrollado. Se realiza un abordaje metacognitivo.
¿Podés verificar el resultado?
¿Podés verificar el razonamiento?
¿Podés obtener el resultado en forma diferente?
¿Podés verlo de golpe?
¿Podés emplear el método en algún otro problema?

También a esta etapa se la conoce como visión retrospectiva. Para construir conocimiento que sirva en el futuro, es necesario observar y reflexionar sobre qué fue lo que se hizo. Así se obtiene un canal de retroalimentación valioso, que ayudará a resolver problemas futuros. Por otro lado, una vez obtenido el método que lleve a una solución correcta, también se procura ver si hay otros métodos alternativos que respondan al mismo problema. De esta manera, se obtienen distintas perspectivas que pueden aplicarse en el futuro.

Ejemplo de aplicación del método de Pólya:

1. Comprender la situación:
una persona compró [condición] medio kilogramo de carne [dato], tres cuartos de kilo de papas [dato] y un cuarto kilo de verduras [dato], ¿cuántos kilogramos transportó a su casa [incógnita]?
2. Elaborar un plan:
sumar lo que se compró y el resultado es la cantidad de kilogramos que la persona tuvo que transportar.
3. Ejecutar el plan:
(1 / 2) + (3 / 4) + (1 / 4) = 6 / 4 = 1,5 kg
4. Revisar, verificar y comunicar:
La persona tuvo que transportar 1,5 kilogramos de comestibles hasta su casa.

Tipos de pensamiento aplicados a la resolución de problemas

Joy Paul Guilford (1950), a finales de los años cuarenta, propuso un modelo de inteligencia que cambió el enfoque tradicional en el análisis de la creatividad, distinguió entre el pensamiento convergente y el pensamiento divergente. El primer tipo de pensamiento, el convergente, se caracteriza por ser analítico y racional, plantea que solo existe una solución correcta para cada problema. Es un pensamiento de tipo cerrado, dado que implica la restricción de las posibilidades y la producción de una única respuesta. Opera basándose en conocimientos previos; la información disponible se ordena de manera lógica para llegar a una solución que resuelve el problema planteado. Se podría decir que en este tipo de pensamiento no se construye el método para obtener esa respuesta, sino que se identifica la correcta (una suerte de reconocimiento de patrones de problemas). Esto implica que su aplicación recurrente no necesariamente garantizaría el desarrollo de la capacidad de resolución de problemas, sino más bien una ejercitación intensiva en detección de tipos de problemas y aplicación de soluciones prediseñadas.

En cambio, el pensamiento divergente se caracteriza por mirar desde diferentes perspectivas y encontrar más de una solución frente a un problema. En esencia, contempla varias opciones de solución, que derivan en respuestas múltiples, que a la vez pueden ser todas correctas o no. La diferencia está dada en que en el pro- ceso se flexibilizan posiciones y se producen nuevas conexiones.Por su apertura en la búsqueda de soluciones es una manera abierta de pensar.

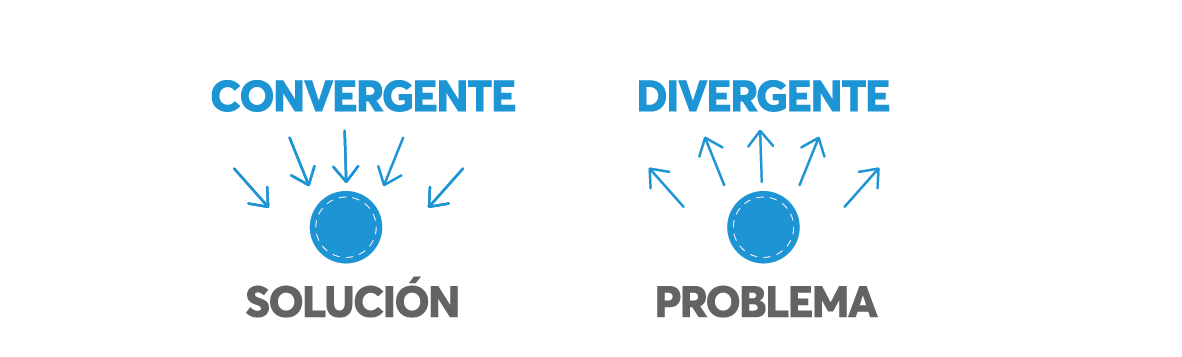
Tipos de pensamiento aplicados a la resolución de problemas

Para Guilford, el pensamiento divergente está formado por una parte importante de creatividad, la cual entendemos como la capacidad de pensar más allá de las ideas admitidas, combinando de una manera original conocimientos construidos, ya que este tipo de pensamiento fuerza la necesidad de generar ideas nuevas. Esto sucede a partir de que, a diferencia del pensamiento convergente, este no se basa en patrones preestablecidos, sino que implica idear un camino nuevo o diferente para resolver el problema. La creatividad implica evitar lo obvio, lo seguro, lo previsible para producir algo que, para su creador, resulte novedoso (Guilford, 1967).

Como explica Guilford, la creatividad no es algo que pocas personas tengan. Por el contrario, es una propiedad compartida por toda la humanidad y está presente en cada individuo en mayor o menor grado. Está relacionada con aptitudes tales como la flexibilidad y la originalidad.
Más allá de las categorías cognitivas establecidas, en la vida real el pensamiento divergente y el pensamiento convergente se complementan y, con ayuda del método heurístico, contribuyen a desarrollar la capacidad para resolver problemas en las personas.
Edward de Bono es un estudioso de las formas de pensamiento aplicadas a la resolución de problemas que ha trabajado intensamente sobre el pensamiento divergente, al que se refiere llamándolo pensamiento lateral. En su definición indica:

“...es una actitud mental y también una cantidad de métodos definidos, la actitud men- tal implica la disponibilidad para tratar de mirar las cosas de diferentes maneras. Implica una apreciación de que cualquier manera de mirar las cosas es sólo una entre muchas. Implica una comprensión de cómo usa la mente los esquemas para poder pasar a otro mejor.” (Del Bono, 1991:29)

En un proceso de resolución de problemas, la exploración, el descubrimiento y la comprensión de las estructuras y las relaciones de los elementos que forman parte del problema son una tarea creativa, en la cual se representa la realidad mediante abstracciones, utilizando modelos. Pero, para salir de la tarea única de reconocimiento de problemas anteriores y producir algo divergente, es decir, creativo, se hace necesaria una actitud crítica y activa, que promueva el trabajo desde diferentes perspectivas.
El pensamiento divergente parte de la base de aceptar que, en temas de enseñanza y de aprendizaje, más allá de las prácticas que giran en torno a la reproducción de saberes, también debe promoverse la construcción de estos.Desarrollar la re- solución de problemas con heurísticas que contemplen ambos pensamientos es una forma de hacerlo.

A modo de síntesis, se puede decir que la creatividad no es simplemente una habilidad aislada del intelecto que sirve para crear cosas nuevas, sino que, por el contrario, surge como una sinergia entre la concepción que se tiene del mundo y su funcionamiento, los conocimientos adquiridos, una gran capacidad analítica y de observación, una percepción abierta del mundo, una actitud permeable que permita reestructurar y modificar construcciones mentales ya establecidas, la predisposición a la posibilidad de equivocarse y a aprender cosas nuevas, una actitud curiosa y comprometida y, por último, un interés en participar del cambio.

Desarrollar prácticas educativas que fomenten el pensamiento divergente y la resolución de problemas implica, por lo tanto, desarrollar también la creatividad y trabajar con todas las características mencionadas anteriormente.
David Bohm, por su parte, desde una posición crítica, coincide con PekkaHimanen (Himanen, 2002) en que estas actitudes son naturales en los niños y que los métodos tradicionales de aprendizaje trabajan en contra del desarrollo de esta capacidad. Y en particular se afirma en dos críticas fuertes: por un lado, declara que en la educación formal no se da espacio al error y esto es contrario a una actitud adecuada hacia este, en la que es importante correr riesgos y aprender de los experimentos y creaciones fallidas; por el otro, afirma que los métodos de aprendizajes memorísticos y rígidos donde se espera una única respuesta producen un aprendizaje anormal donde se forman estructuras mentales que no son propicias para ser reutilizadas en diversos contextos (Bohm, 2002).

La creatividad y los problemas en la escuela

El término creatividad ha aparecido varias veces en el texto ligado a las situaciones de resolución de problemas. Este hecho dota al concepto de una importancia particular ya que se la percibe como una actitud a desarrollar para lograr el desarrollo del pensamiento divergente. Por otro lado, es considerada actualmente una característica que servirá como herramienta a los estudiantes el día de mañana en su inserción en el ámbito laboral.
El profesor Mitchel Resnick, director del proyecto Lifelong Kindergarten en el MIT Media Lab, afirma:

“En el mundo rápidamente cambiante de hoy, la gente debe continuamente crear soluciones creativas a problemas inesperados. El éxito se basa no solo en lo que tú sabes o cuánto sabes, sino en tu habilidad de pensar y actuar creativamente.” (Resnick 2007a)

Por este motivo, desarrollar una actitud creativa resulta de interés también para las instituciones educativas, donde no suelen ejercitarse estas aptitudes. El traba- jo escolar se centra, por lo general, en resolver problemas específicos, por lo que luego resulta muy difícil poder aplicar y adaptar estas soluciones como respuesta a problemas inesperados o diferentes.

Así mismo, las nuevas tecnologías proporcionan una oportunidad para desarrollar tal actitud ya que permiten crear producciones en gran variedad de formatos (digitales o físicos) y proporcionan también plataformas digitales donde compartirlas y seguir construyéndolas de manera colaborativa. En su trabajo con jóvenes y adolescentes en el MIT Media Lab, Resnick ha identificado, presenciado y destacado la importancia de jugar y explorar con herramientas digitales como una forma de promover una actitud creativa y activa (Resnick, 2007b).
Por otro lado, Stager también destaca que las tecnologías digitales proporcionan un marco propicio para ejercitar esta actitud ya que son requeridas en todos los proyectos emprendidos en las prácticas maker1 (Stager, 2014).

Más allá de los autores mencionados, es relativamente fácil encontrar bibliografía con temáticas vinculadas a la creatividad en el ámbito laboral.Esto se ve potenciado, en parte, por la velocidad de los cambios en el mundo actual que genera la necesidad de una continua adaptación, enfrentando a los ciudadanos a situaciones y oportunidades que no existían en el momento de su formación.

Los procesos de automatización han mejorado la capacidad productiva tanto de la industria como de la agricultura, han influido en las formas y en la cantidad de empleos disponibles, y se espera que su mayor impacto se produzca en las décadas venideras. Se prevé que, en los próximos 20 años, el 47 % de los empleos actuales desaparezcan a causa de la automatización, la inteligencia artificial y la robótica (Fresneda, 2016).Esto no significa, sin embargo, que existirán un 47 % menos de empleos disponibles, sino que las nuevas tecnologías darán paso a nuevos tipos de empleos que requerirán, a su vez, nuevas habilidades y mayor formación. Entre estas habilidades revalorizadas, que son transversales a todas las disciplinas, se destacan: el aprendizaje continuo, la predisposición para trabajar en equipo, la adaptación al cambio y, por sobre todo, la creatividad (WEF, 2016).
El informe The future of jobs.Employment, skills and work for strategy for the fourth industrial revolution del Foro Económico Mundial, indica que en el horizonte 2020 se prevén cambios disruptivos en el set de habilidades que los trabajadores necesitarán para poder integrarse en el mundo laboral. Incluso afirma que no será suficiente con adaptar o modernizar contenidos curriculares y cátedras universitarias ya que la vida útil de las habilidades requeridas para un mismo empleo es demasiado corta y los trabajadores deberán estar en un continuo estado de aprendizaje y adaptación. En este contexto, la capacidad de encontrar soluciones a nuevos problemas y de pensar de manera lateral y original no solo será necesaria para la diferenciación del ciudadano de cara al mercado laboral humano, sino también frente a posibles automatizaciones en torno a su empleo.

En este capítulo, se han presentado algunos conceptos básicos que deberían es- tar presentes en las aulas más a menudo y que hacen hincapié en las posibilidades educativas del hacer, entendido como una forma de construir conocimientos profundos que comienzan en las manos del aprendiz. En el siguiente capítulo, avanzaremos en el tema central de este libro y presentaremos el concepto denominado pensamiento computacional, como así también las capacidades implica- das en su desarrollo. Trataremos de llevar las reflexiones hacia la oportunidad de poder incorporar el PC en el aula con la finalidad de dar a los aprendices nuevas herramientas cognitivas que les permitan comprender y habitar problemas de una mejor manera.